
Before we can talk about angles, we should talk about lines. We can describe the relationship between two lines in two ways: parallel or intersecting. Parallel lines are lines that travel in the same direction and will never cross. Intersecting lines are lines that have different slopes and therefore cross each other. When this intersection forms a right angle, we call the lines perpendicular.

The spaces between intersecting lines are called angles. There are three different classifications for angles: acute, obtuse, or right. Angles less than 90 degrees are called acute angles. Angles greater than 90 degrees are called obtuse angles. Angles that are exactly 90 degrees are called right angles.

Another word we could use for a shape is a polygon. A polygon is any figure made up of straight lines that form a closed shape. Polygons are named based on how many sides they have. They can have a regular shape or an irregular shape. The following table introduces the different polygon names and descriptions:

Other terms you should know about shapes:
Equilateral - all sides are the same length
Equiangular - all angles have the same measure
Types of Triangles
Triangles can be classified in different ways. One way uses the angles of the triangle. If one angle is exactly 90 degrees, it is called a right triangle. If all of the angles are less than 90 degrees, it's an acute triangle. If one angle is greater than 90 degrees, then it's an obtuse triangle. When all of the angles have the same measure, it is an equiangular triangle.
Another way to classify triangles is by using the lengths of the sides. When exactly two sides have the same length, it's an isosceles triangle. When all three sides have the same length, it's an equilateral triangle. When no sides have the same length, it's called a scalene triangle.

Characteristics of Triangles
An important characteristic you should know about triangles is that the sum of the angles inside the triangle must always equal 180 degrees. You can use this information to help you solve for the measure of an unknown angle. Consider the following example:
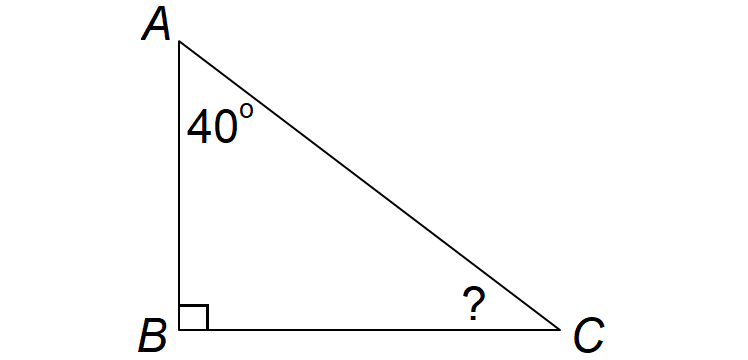
The square in the B corner indicates that it is a right angle. Recall that right angles are exactly 90 degrees. We know that A + B + C = 180. Substituting the degrees we do know, we can rewrite that as: 40 + 90 + C = 180. Now we can solve for C through simplification. First, we can combine like terms: 40 + 90 = 130. So, 130 + C = 180. Now we move the 130 to the other side of the equation by performing the inverse (or opposite) operation. That means we will subtract it from both sides leaving: C = 50. So the measure of angle C equals 50 degrees.
Another important characteristic is that the angles across from sides of equal lengths have equal measures. In other words, if two sides have the same length, the angles across from them will also have the same measure. Consider the following example:
The marks on the sides indicate that they are congruent or have the same length. Since they have the same length, the bottom angles have the same measure. We know that the sum of the three angles must equal 180, so we can think of it as: 30 + x + x = 180. If we combine like terms, we can rewrite that as: 30 + 2x = 180. Now we solve for x by isolating x on one side of the equation. We do this by moving everything else to the other side using inverse operations. We start with the 30 since it isn't attached to the x term. We move it by subtracting it from both sides, and we get: 2x = 150. Now we move the 2 by dividing it on both sides: x = 75. So, the measure of each angle on the bottom of the triangle is 75 degrees.
Types of Quadrilaterals
Any shape that has four sides is called a quadrilateral. When the shape has two pairs of parallel sides, it's called a parallelogram. A trapezoid has one pair of parallel sides. When all of the sides have the same length, and there are two pairs of parallel sides, we call it a rhombus. When all of the angles are 90 degrees, and there are two pairs of sides with equal length, it's a rectangle. A square is like a rectangle, except all of the sides have equal length.

Characteristics of Parallelograms
Unlike triangles, the sum of the inside angles in a parallelogram is equal to 360 degrees. Quadrilaterals can also be conceptualized as being composed of triangles of different shapes. This will be explored more in another section.
Perimeter
When we add up (sum) the lengths of the sides of a shape, we are computing the perimeter of that shape. Consider the following shape:
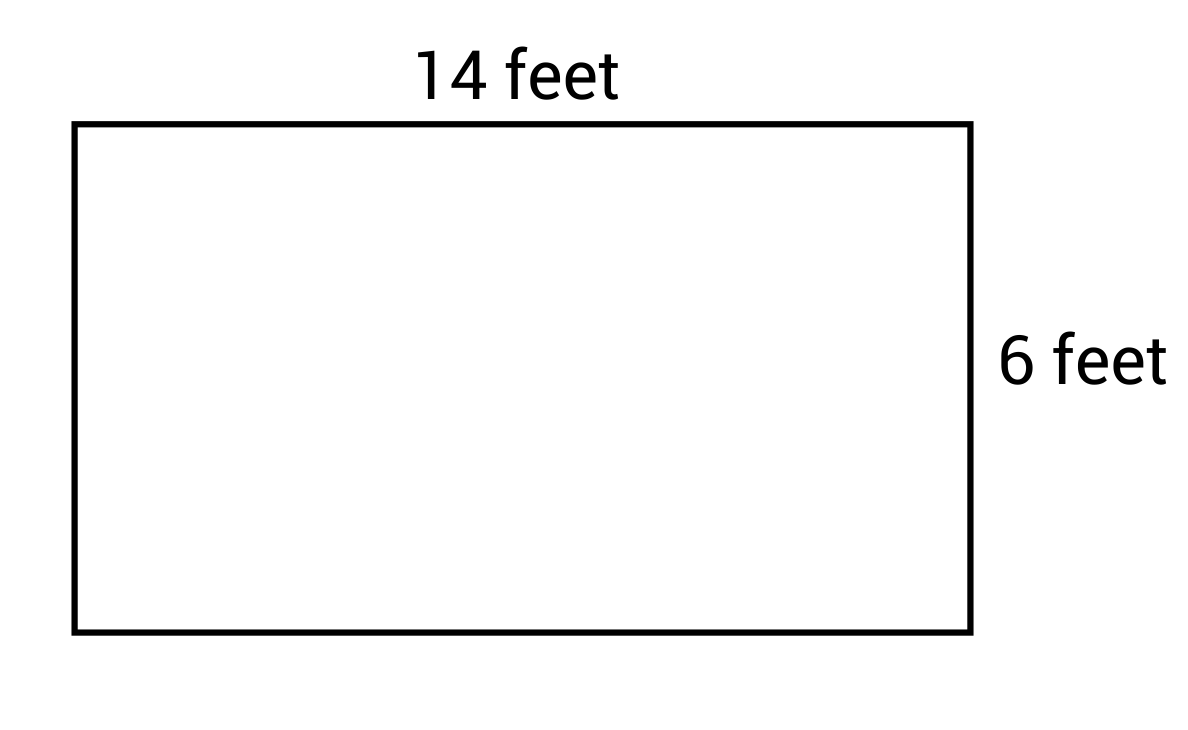
The shape is a rectangle, so we know that opposite sides have equal lengths. That means there are two sides that measure 14 feet long and two sides that measure 6 feet long. To find the perimeter, we sum all of those lengths: 14 + 14 + 6 + 6 = 40 feet. Be sure that you're including a label (i.e., units of measurement) with your answer: The perimeter of the rectangle is 40 feet.
Now let's consider a more complex example:
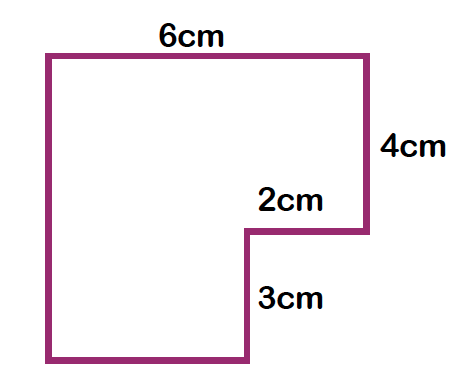
In this shape, the lengths of two of the sides are not given to us. So, before we can compute the perimeter, we need to determine the length of those two sides. One method for finding this is to consider this shape as a regular shape, or perhaps two regular shapes if you prefer.

In this way, we can see that the small shape in the bottom corner has two pairs of equal sides, like a rectangle. The same can be said of the larger shape. That means that the bottom unknown length plus the 2cm must equal 6cm, since that is the length of the opposite side: x + 2 = 6 or x = 4. So, we know that the length of the bottom side is 4cm. We can apply the same logic to finding the missing length of the left side. We know it must be equal to the opposite side: 4cm + 3cm = 7cm. So, the length of the left side is 7cm.

Now that we know all of the lengths, we can add the sides to find the perimeter of the original shape: 6 + 7 + 4 + 3 + 2 + 4 = 26. So the perimeter of the shape is 26cm.
Circumference
The perimeter of a circle is also known as its circumference. Since circles do not have straight sides, we cannot find the circumference by simply adding up the length of each side. Instead, we can use a formula for computing the circumference. The computation can be done using the diameter of the circle or its radius. So, before we get to the formulas, let's talk about radius and diameter.
Radius & Diameter
The radius (r) is the distance from the middle of the circle to any point on the edge of the circle. Since circles are uniform in shape, this distance will be the same at every point around the circle. The diameter (D) is the distance from one side of the circle to the other side, cutting through the center of the circle. We could also conceptualize the diameter as being twice as long as the radius. Similarly, we can think of the radius as being half the length of the diameter.

Pi
Before we can look at the formulas for computing the circumference, I need to introduce one more concept: pi (π). If you divide the circumference of a circle by its diameter, you always get the same result, which we call pi. Pi (π) is approximately equal to 3.14. Since the value of pi never changes, pi is a mathematical constant. Many calculators include a π button that you can use for more precise calculations.
Formulas
There are two ways that you can compute the circumference, one using the diameter and one using the radius. If we have the diameter, we can simply multiply that value by π to find the circumference. For example, if the diameter of the circle was 5 cm, then the circumference is 5 x π or approximately 15.71cm.
If we understand that the diameter is twice the length of the radius, then it comes as no surprise that we can find the circumference by taking π times 2 x radius. For example, if the radius of the circle was 5cm, then the circumference would be 2 x 5 x π or approximately 31.42 cm.

© Copyright 2025 National University. All Rights Reserved.